

在各种测量中,都需要应对噪声,噪声的产生原因各有不同,而其数学分布有一定规律。本文简单介绍了噪声的几种数学分布,对噪声
的处理有一定作用。
在使用探测器、相机等器件时,都需要应对噪声。噪声具有统计学上的特征属性。可以通过概率密度函数进行分类。
(1)高斯噪声
高斯噪声是指它的概率密度函数服从高斯分布的一类噪声。
概率密度函数PDF:

其中μ为平均值或期望值,σ为标准差,σ2为方差。
产生原因:1)图像传感器在拍摄时市场不够明亮、亮度不够均匀;2)电路各元器件自身噪声和相互影响;3)图像传感器长期工作,温度过高。
(2)瑞利噪声
概率密度函数PDF:
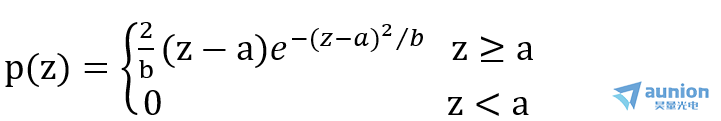

(3)伽马噪声
概率密度函数PDF:

其中,a>0,b为正整数。
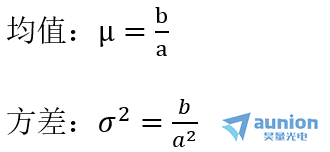
(4)指数分布噪声
概率密度函数PDF:
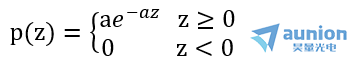
其中a>0。
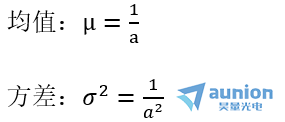
(5)均匀噪声分布
概率密度函数PDF:
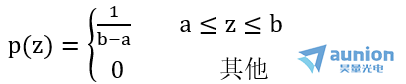
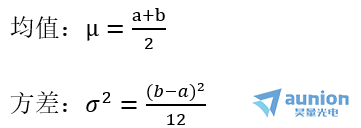
(6)脉冲噪声(椒盐噪声)
概率密度函数PDF:

如果b>a,灰度值b在图像中将显示为一个亮点,相反,a的值将显示为一个暗点。若Pa或Pb为零,则脉冲噪声称为单极脉冲。如果Pa
和Pb均不可能为零,尤其是它们近似相等时,脉冲噪声值将类似于随机分布在图像上的胡椒和盐粉微粒,因此称为椒盐噪声。它们有
时也称为散粒和尖峰噪声。
噪声有其功率谱密度函数,可以通过功率密度分类噪声。介绍两种常见的噪声。
白噪声是一种功率谱密度为常数的随机信号。此信号在各个频率上的功率谱密度是一样的,因此这种信号也被称作白噪声。相对的,其
他不具有这一性质的噪声信号被称为有色噪声。
粉红色噪声又被称做1/f噪音,因为它的能量分布与频率成反比,每一次频率翻倍能量就衰退3dB,因此也被称作低频噪声。
展示全部 
