Chirp-z变换是Lawrence Rabiner在1968年对语音信号进行分析时提出来的，它可以将z平面的单位圆变成一个螺旋线逐渐地从单位原
点到单位圆内。信号谱分析可以在z平面上的螺旋线上实现，可以开始于任意一点，结束于另一任意点。
数字信号左傅里叶变换，频域的采样点数是固定的，若要更多的频率，需要在时域部分添加零，但同时带来的问题是消耗更多的时间。
当只是观察频域中的某一部分，又想看到更加详细的内容时，可以使用CZT变换。
离散傅里叶变换公式如下
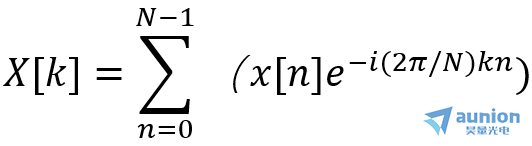
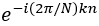表示一个离散的正弦波，基频时2π/N，k时一个整数，表示正弦信号的频率是基频的k倍。
傅里叶变化的频谱角度看，它的抽样点为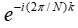 
，在坐标系下可以表示为
CZT_4
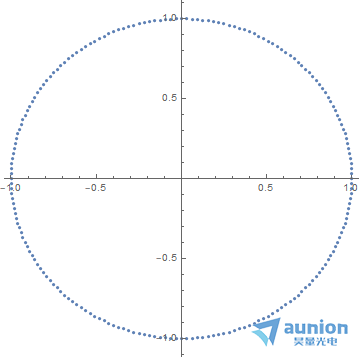
从上图可以看到，傅⾥叶变化的频率，是对⼀个单位圆上进⾏等间隔的抽样。若要看到更多 的细节，需要在不改变原始信号的情况
下，在周围补零的操作，增加信号的⻓度，如下所⽰，从⼀百个点增加到200个点，可以看到频谱的点数增加了⼀倍，考到的频谱曲线
会更加详细。
CZT_6
但是补零的操作会增加数据量，计算消耗的时间约更⻓，因此需要采⽤⼀种更加通⽤的形 式，只观察需要的部分。
傅里叶变化中的正弦波都是用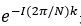
来表示，这里可以采用
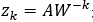来替代，其中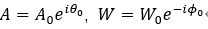
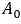是矢量半径的起始长度
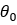表示抽样点的起始位置
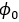是点的抽样间距，当
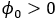时，抽样点逆时针旋转，当
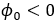时，抽样点顺时针旋转
可以表示螺旋线的方向，当
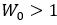螺旋线向内收缩，当
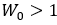螺旋线向外伸展，
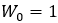表示一个单位圆。傅里叶变换就是这种特殊情况。
采用这种方式的时候，通常采样的频率时螺旋型的，而且密度可以任意设置，观察的区域更加灵活
另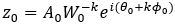
，相对于傅里叶变化，这是一种更加通用的方式
根据布鲁斯特等式
，所以
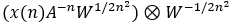表示卷积，计算卷积通常是先计算他们的FFT，然后求IFFT
另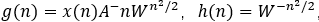
若要在信号取样的点数为M，那么整个序列的长度应该为L≥M+N-1，在计算FFT的时
候，序列点数最好取2的m次方，所以L满足L=2^m，因此，上述两个式子可以具体表述为
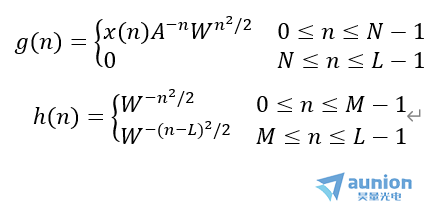
举例
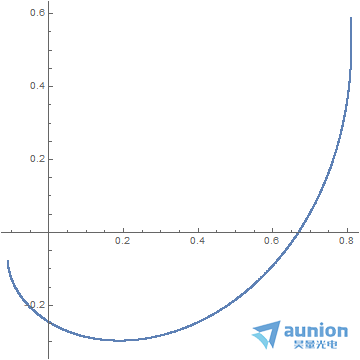
以一个Rect函数作为信号，演示CZT变换
对模拟信号进行傅里叶变换后得到频谱信息
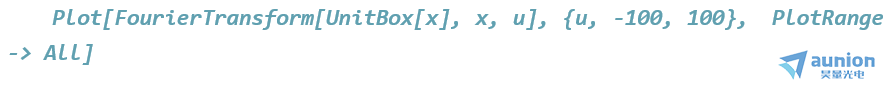
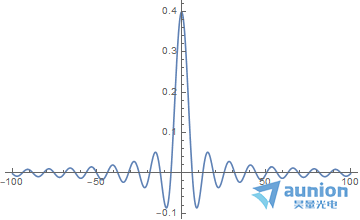
若对信号进行采样，假设原始信号1对应1s，那么原来的信号长度为2s，采样的间隔为0.05s
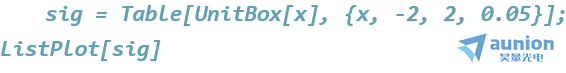
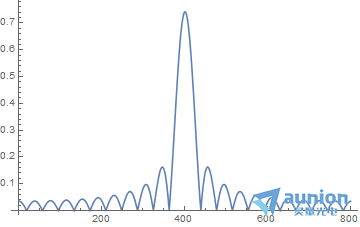
傅里叶变换后得到的频谱是
横坐标每一格实际大小是10/81 Hz，最高频率是5Hz
如果要增加傅里叶变化后的分辨率，可以在信号两边填充零
横坐标每一格实际大小是10/801 Hz，最高频率是5Hz
补零不影响最高频率，只是增加频率的分辨率
CZT计算某一段的频谱
原始信号为
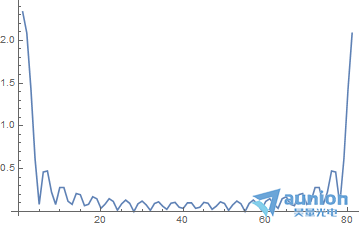
信号的总长度是81， 第一个点对应频率DC，81个点对应的相位应该是0到2[Pi]*80/81，我们取点1-20之间的区域作为放大的区域
因此基本的参数如下，原始的信号长度
n1=81
对应的最终相位是2[Pi]*19/81，假设需要的长度是
m1=200
那么抽样的分辨率是
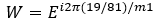
起始位置为零，因此
A=1
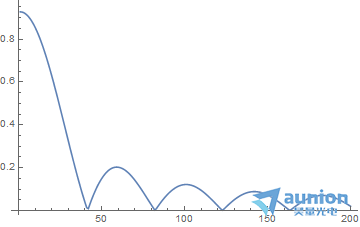
数据的总长度是
L=m1+n1-1=280
因此另L=512
分别计算g和h
您可以通过我们的官方网站了解更多的产品信息，或直接来电咨询4006-888-532。
展示全部 
展示全部
